
This could both be beneficial, because calls to non-builtin functions inside a loop prevent Matlab's JIT compiler from translating the loop to machine language. Learn more about realmax, realmin The following is expected behavior for realmax: > realmax ans 1.797693134862316e+308 > realmax2 ans Inf But the following is unexpected behavior for realmin (a.
Also, roots does nothing more than find the eigenvalues of the companion matrix, so you could find these eigenvalues yourself, which prevents a call to roots. realmax is really real max, but is realmin.

This allows you to find only one (or a few) roots and save time (there's a fair chance it's also possible to compute the roots or extrema of a Chebychev analytically, although I could not find a good reference for that (or even a bad one for that matter.)).Īnother attempt that you can make in speeding things up, is to note that polyder does nothing more than Pprime = (numel(P)-1:-1:1). You can modify the eig evaluation of the companion matrix in there, to eigs. It does so by interpolating the polynomial by a Chebychev polynomial, and finding its roots. There is a file exchange submission by Steve Morris which finds all real roots of functions on a given interval. If A is a vector, then max (A) returns the maximum of A. I could be completely wrong here but you might just be out of luck in getting something faster unless you can provide more information of have some kind of relationship between the polynomials generated at each step. Description example M max (A) returns the maximum elements of an array. There is insufficient information available to consider calculating just a subset of roots of the derivative polynomial - how could you know which derivative root provides the maximum stationary point of the polynomial without comparing the function value at ALL of the derivative roots? If your polynomial coefficients were being perturbed at each step by only a (bounded) small amount or in a predictable manner, then it is conceivable that you would be able to try something iterative to refine the solution at each step (for example something crude such as using your previous roots as starting point of a new set of newton iterations to identify the updated derivative roots), but the question does not suggest that this is in fact the case so I am just guessing. This is equal to realmax for double precision, and to single ( (2-2 (-23))2127) for single precision. f realmax (precision) returns the largest finite floating-point number in IEEE single or double precision. If the coefficients of the polynomial change at every time step in an arbitrary fashion, then ultimately you are faced with a distinct and unrelated optimisation problem at every stage. f realmax returns the largest finite floating-point number in IEEE double precision. The max function ignores NaNs.I think that you are probably out of luck.
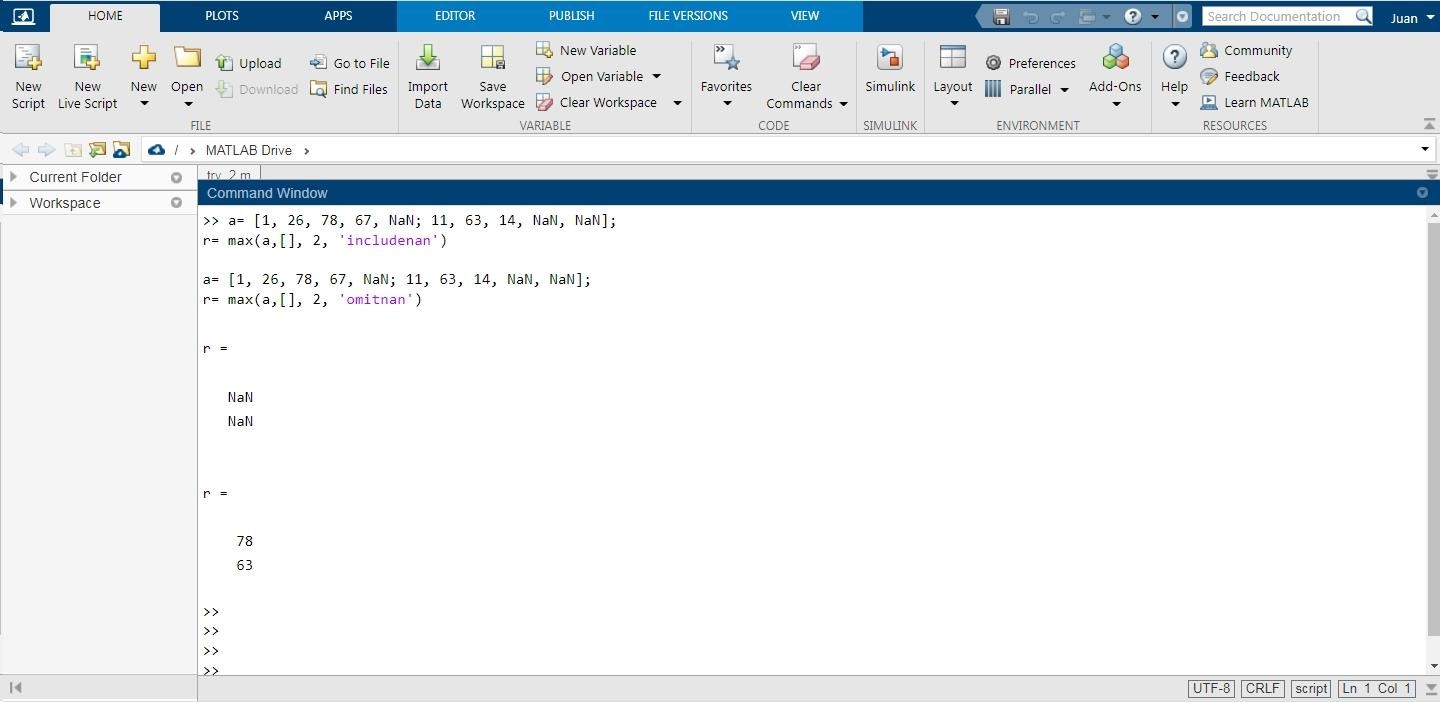
If there are several identical maximum values, the index of the first one found is returned.įor complex input A, max returns the complex number with the largest complex modulus (magnitude), computed with max(abs(A)), and ignores the phase angle, angle(A). For example, max(A,1) produces the maximum values along the first dimension (the rows) of A.įinds the indices of the maximum values of A, and returns them in output vector I. Returns the largest elements along the dimension of A specified by scalar dim. Returns an array the same size as A and B with the largest elements taken from A or B. If A is a multidimensional array, max(A) treats the values along the first non-singleton dimension as vectors, returning the maximum value of each vector. If A is a matrix, max(A) treats the columns of A as vectors, returning a row vector containing the maximum element from each column. If A is a vector, max(A) returns the largest element in A. The following is expected behavior for realmax: Theme Copy > realmax ans 1. Returns the largest elements along different dimensions of an array. f realmax returns the largest finite floating-point number in IEEE ® double precision. Max (MATLAB Functions) MATLAB Function Reference


 0 kommentar(er)
0 kommentar(er)
